7. Obojsmerný lineárny zoznam
7.2 Problém – Faktoriál
Vytvorte program na výpočet hodnoty n! (n-faktoriálu) s využitím vhodnej dynamickej údajovej štruktúry.
Riešenie
Program na výpočet faktoriálu pre dané prirodzené číslo n nechýba v úvode žiadneho kurzu programovania.
Ak vám niekto „prikáže naprogramovať faktoriál,“ spomeniete si na matematickú definíciu:
a po chvíli je na svete program:
int n, i;
unsigned int fakt = 1;
scanf("%d", &n);
for (i = 1; i <= n; i++) fakt *= i;
printf("%d ! = %d", n, fakt);
Algoritmus je síce v poriadku, avšak program bude fungovať len ak n<13. Prečo? Ak údajový typ unsigned int zaberá v pamäti 4 bajty, tak výsledná hodnota 13! = 6227020800 je už väčšia ako maximálna prípustná hodnota tohto typu. My však chceme určiť hodnotu n! pre veľké n – koľko je 100!, 789!, 1500! … ? Zaujímať nás bude navyše nielen samotná hodnota výsledku, ale i počet cifier.
Pri riešení využijeme dynamickú údajovú štruktúru obojsmerný lineárny zoznam. Cifry faktoriálu budú uložené v jeho prvkoch – v programe ich vypočítame „manuálne“ postupným násobením cifru po cifre s pamätaním prenosu. Algoritmus okrem iného spôsobu uchovávania hodnoty faktoriálu v podstate kopíruje „tradičné“ riešenie s využitím cyklu so známym počtom opakovaní. Postupujeme takto:
Najskôr si pripravíme údajovú štruktúru, v ktorej budeme priebežne uchovávať medzivýsledok. Pôjde o obojsmerný zoznam prvkov typu TPrvok:
typedef struct prvok {
char cifra;
struct prvok *predch;
struct prvok *nasled;
} TPrvok;
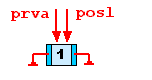
Prvý prvok zatiaľ nemá predchodcu ani nasledovníka, prvá cifra je zároveň poslednou (keďže je jediná 🙂).
Potom už zrealizujeme vlastný výpočet. Postupne v cykle for vypočítame hodnotu 1!, 2!, 3!, …, (n − 1)! a v poslednom opakovaní napokon n!
Nech n = 8. Na obrázku je znázornený zoznam po výpočte hodnoty 7! = 5040:
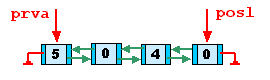
Počítajme teraz hodnotu 8! = 8.7!
Násobíme od poslednej cifry, pomocný ukazovateľ preto nastavíme na posledný prvok v zozname:
cislica = posl;
násobíme:
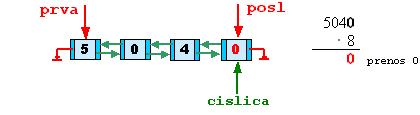
cislica = cislica->predch;
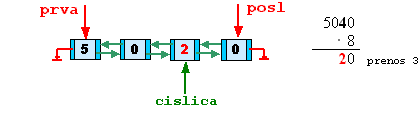
cislica = cislica->predch;
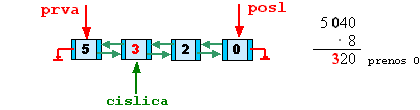
cislica = cislica->predch;
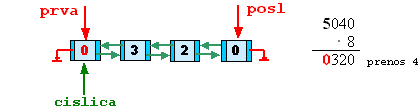
Prešli sme postupne celým zoznamom. Posledný prenos je ale rôzny od nuly. Preto pridáme na začiatok zoznamu nový prvok (ďalšiu cifru):
cislica = (TPrvok*)malloc(sizeof(TPrvok));
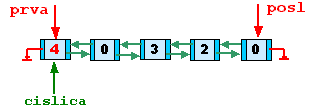
Pridať nový prvok znamená nielen alokovať pamäť, ale aj naplniť jeho hodnotovú časť príslušnou cifrou a nastaviť správne ukazovatele. Prvok pridávame na začiatok – predchodcu teda nemá. Aktualizujeme aj hodnotu ukazovateľa na prvú cifru (máme nový začiatok zoznamu).
Voľba údajovej štruktúry sa ukázala výhodná – v jednom smere prechádzame zoznamom pri násobení po cifrách, v opačnom smere pri výpise výsledku.
Pre väčšie n nemusí byť posledný prenos jednociferné číslo! Na začiatok pôvodného zoznamu sa potom pridáva viac cifier (nových prvkov). Počet cifier výsledku môžeme zistiť pri výpise výsledku na obrazovku.
