9. Stromy

9.5 Binárny vyhľadávací strom

Veľmi užitočným prípadom binárneho stromu je tzv. binárny vyhľadávací strom (binary search tree). Využíva sa výhodne v mnohých triediacich a vyhľadávacích algoritmoch, kde sa kladie dôraz na rýchlosť. Má špeciálnu vlastnosť:
 
Vrcholy stromu sú ohodnotené celými číslami. Pre každý vrchol platí, že v ľavom synovi je uložená menšia a v pravom synovi hodnota väčšia ako v danom vrchole. Je teda charakteristický tým, že všetky hodnoty v ľavom podstrome sú menšie a v pravom podstrome zase väčšie ako hodnota v koreni stromu. To isté platí pre ľubovoľný podstrom.
 
Na obrázku je príklad binárneho vyhľadávacieho stromu:
 

 
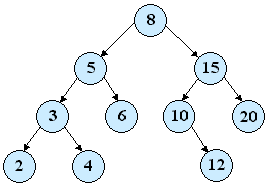
Napíšeme funkciu na vloženie novej hodnoty do binárneho vyhľadávacieho stromu:

typedef struct vrchol {
	int info;
	struct vrchol *ls, *ps;
} TVrchol;


void vloz(TVrchol **koren, int x)
{
	if (*koren == NULL) {
		*koren = (TVrchol*)malloc(sizeof(TVrchol));
		(*koren)->info = x;
		(*koren)->ls = NULL;
		(*koren)->ps = NULL;
	}
	else {
		if (x < (*koren)->info) vloz(&((*koren)->ls), x);
		else vloz(&((*koren)->ps), x);
	}
}

Pozor!
Prvý parameter musí byť volaný odkazom – t. j. ide pointer na pointer na typ TVrchol. Pri vkladaní nového prvku ako syna nejakého vrcholu musíme totiž po jeho vytvorení v pamäti nastaviť v otcovi príslušný ukazovateľ! Ukazovateľ na pridaný vrchol sa vyvezie „o poschodie“ vyššie.

Či sa nejaká hodnota nachádza v binárnom vyhľadávacom strome, môžeme zistiť iteračne. Prechádzame stromom od koreňa, pokračujeme v jednom z podstromov, podľa toho, či je hľadaná hodnota väčšia alebo menšia ako hodnota v koreni. Funkcia najdi vracia ukazovateľ na nájdený vrchol resp. NULL ak sa vrchol s takou hodnotou v strome nenachádza. 

TVrchol *najdi(int x, TVrchol *koren)
{
	int najdeny = 0; /* false */

	while ((koren != NULL) && (!najdeny)) {
		if (koren->info == x) najdeny = 1; /* true */
		else if (x < koren->info) koren = koren->ls;
			else koren = koren->ps;
	}
	return (koren);
}

Rušenie vrcholov môžeme považovať za inverzný problém k pridávaniu vrcholov do stromu. Je však o niečo zložitejší. Ak je vrchol listom alebo má jediného syna, riešenie je jednoduché:
 
Zrušenie vrcholu bez synov:
Potrebujeme poznať ukazovateľ na otca rušeného vrcholu. Nech je to smerník v a chceme zrušiť jeho ľavého syna. Stačia na to dva príkazy:


 
free((void*)v->ls);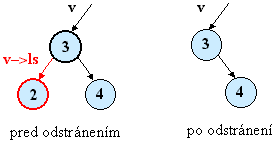
v->ls = NULL;
 

Zrušenie vrcholu s jediným synom:
Potrebujeme poznať ukazovateľ v na otca rušeného vrcholu. Ten nech je napr. jeho ľavým synom. Nech má rušený vrchol jediného napr. pravého syna. Zapamätáme si ukazovateľ na rušený vrchol (on), prepojíme otca s novým synom a zrušíme príslušný vrchol:


on = v->ls;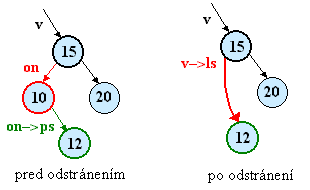
v->ls = on->ps
free((void*)on);
 

Situácia sa skomplikuje, ak potrebujeme odstrániť vrchol, ktorý má dvoch synov (je vo vnútri stromu) – nemôžeme predsa nahradiť jeden smerník dvoma! Preto sa v takýchto prípadoch rušený prvok nahradí buď najpravejším prvkom ľavého podstromu alebo najľavejším prvkom pravého podstromu.

Ak by sme chceli zo stromu na úvodnom obázku odstrániť napr. vrchol s hodnotou 15, nájdeme najpravejší prvok jeho ľavého podstromu – má hodnotu 12. Nahradíme hodnotu 15 novou hodnotou a najpravejší vrchol zrušíme. Ak by mal najpravejší vrchol ľavého syna, nastavíme ešte príslušný ukazovateľ vo vrchole 10 na tohto syna resp. na NULL ak žiadneho nemá (ako v tomto prípade).
 


Uvedená funkcia rozlišuje všetky tri spomenuté prípady:

TVrchol *on;  /* ukazovateľ na rušený prvok */

void nahrad(TVrchol **v)   /* pomocná funkcia */
{
	if ((*v)->ps != NULL) nahrad(&(*v)->ps);
	else {
		on->info = (*v)->info;
		on = *v;
		*v = (*v)->ls;
	}
}

void odstran(int x, TVrchol **koren)
{
	if (*koren == NULL) printf(„Take cislo v strome nie je\n“);
	else {
		if (x < (*koren)->info) odstran(x, &(*koren)->ls);
		else if (x > (*koren)->info) odstran(x, &(*koren)->ps);
			else {
				on = *koren;
				if (on->ps == NULL) *koren = on->ls;
				else if (on->ls == NULL)  *koren = on->ps;
					else nahrad(&on->ls);
				free((void*)on);
			}
	}
}

Funkcia nahrad sa volá len v treťom prípade – nájde najpravejší prvok ľavého podstromu, nahradí hodnotu rušeného vrcholu, pripraví situáciu na odstránenie najpravejšieho prvku v ľavom podstrome (zmení hodnotu ukazovateľa on).

Precvičme si

Výškou stromu rozumieme dĺžku cesty od koreňa k najvzdialenejšiemu listu. Ak je koreň na prvej úrovni, jeho synovia na druhej atď., tak najvzdialenejší list bude na úrovni h + 1. Koľko vrcholov môže mať najviac binárny vyhľadávací strom, ak má výšku h?

[Riešenie]

Vytvorte program, ktorý pomocou menu umožní pracovať s binárnym vyhľadávacím stromom. Využite vyššie uvedené funkcie a doplňte funkcie na výpis všetkými troma metódami. Nakreslite binárny vyhľadávací strom, ktorý vznikne pridaním desiatich prvkov do prázdneho stromu takto:
 
for (int i = 1; i <= 10; i++) vloz(&strom, i);
 
Prezradíme, že ide o tzv. degenerovaný strom. Ako vyzerá?

[Riešenie]