9. Stromy

9.7 Triedenie haldou

Na záver kapitoly o stromoch si priblížime jednu z rýchlych metód vnútorného triedenia (triedenia na mieste), ktorá využíva stromovú dynamickú údajovú štruktúru nazývanú halda (hromada, heap). Ide o triedenie haldou – Heapsort.

Halda je binárny strom so špeciálnymi vlastnosťami:

  • usporiadanie – pre každý vrchol platí, že jeho hodnota je väčšia (nanajvýš rovná) ako hodnoty všetkých jeho potomkov
  • tvar – každý vrchol, ktorý nie je na predposlednej alebo poslednej úrovni má dvoch synov. Na predposlednej úrovni sú zľava najskôr vrcholy s dvoma synmi, potom vrchol majúci iba ľavého syna a nakoniec vrcholy bez synov (listy).
Triedenie prebieha v dvoch fázach:

1. fáza  – vytvorenie haldy

Prvky vstupnej postupnosti, ktorú chceme triediť uložíme postupne do binárneho stromu.
 

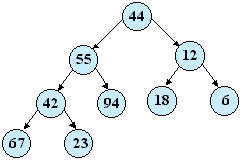vstupná postupnosť: 44, 55, 12, 42, 94, 18, 6, 67, 23


Haldu získame postupnou výmenou obsahov vrcholov. Vychádzame z listov a vždy keď narazíme na vrchol s menšou hodotou ako hodnota aspoň jedného jeho syna, výmenou hodnôt ho necháme klesnúť.
 
OBRÁZOK


Na obrázku je znázornená výsledná halda:
 

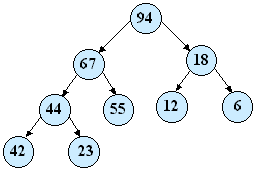
2. fáza  – výpis prvkov haldy

V koreni sa nachádza najväčší prvok postupnosti. Vypíšeme ho a potom ho odstránime – na jeho miesto uložíme najvzdialenejší prvok stojaci vpravo dolu. Obnovíme haldu – koreňový prvok „spustíme“ na správne miesto. Opakujeme, kým sa halda nevyprázdni. Prvky odstránené v tomto poradí tvoria utriedenú postupnosť.

Odstránime 94
Na jeho miesto uložíme 23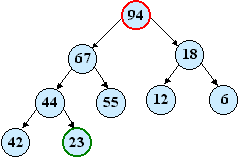
 
Číslo 23 necháme klesnúť.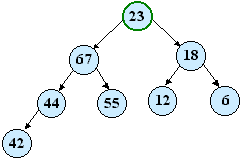
 
 

 
 
Odstránime 67.
Na jeho miesto uložíme 42.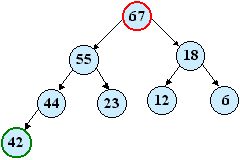
 
Číslo 42 necháme klesnúť atď.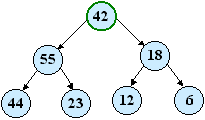
 
 

Implementácia haldy pomocou poľa

Halda sa dá jednoducho implementovať pomocou poľa. Prvky haldy sa do poľa uložia po riadkoch – úrovniach stromu.
 
 

Prvok A[i] má synov A[2i] a A[2i+1], prvok A[i/2] je otcom A[i]
Pre každé i = 2, … , n platí: A[i/2] >= A[i]

Namiesto toho, aby sme odstránili koreň A[1], vymeníme ho s A[n]. Zmenšíme n o jedna a nový prvok A[1] necháme klesnúť v poli A[1], …, A[n − 1] na správne miesto.

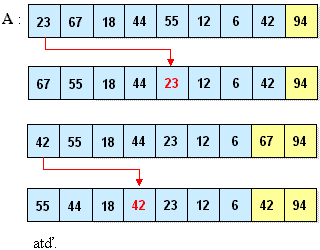
Na konci poľa sa vytvára z najväčších prvkov usporiadaná postupnosť!

[Program]

Triedenie haldou je vylepšením triedenia priamym výberom. Výhodou je to, že v koreni haldy je vždy maximálny prvok, nemusíme ho hľadať a preto je algoritmus rýchlejší.
 
Dá sa dokázať, že haldu možno vytvoriť v O(n·log2n) krokoch a pokles prvku z koreňa vyžaduje najviac O(log2n) krokov. Heapsort je teda triediacim algoritmom s časovou výpočtovou zložitosťou O(n·log2n) .