Pracovný list "Archimedov zákon"

1. Klikni na odkaz Applet Archimedov zákon oboznám sa s appletom, pozoruj pozorne applet a zamysli sa nad jeho významom.

2. Klikni na Applet Archimedov zákon, na základe experimentovania zapíš do tabuľky, aká je vztlaková sila pri ponáraní telesa objemu 5 dm3, hustote telesa 2400 kg/m3 (sklo), hustote kvapaliny 998 kg/m3 (voda) a tiažovom zrýchlení na Zemi 9,81 m/s2. Stláčaj tlačidlo „Krok vpred“ a pre príslušný ponorený objem zapíš hodnoty do tabuľky zaokrúhlený na dve desatinné miesta.

Ponorený objem telesa (dm3)

1

2

3

4

5

Vztlaková sila (N)



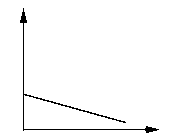
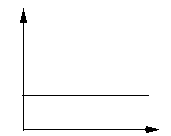
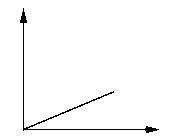
3. Zvážte, či vztlaková sila s ponoreným objemom rastie alebo klesá. Vyberte správne grafické vyjadrenie závislosti vztlakovej sily od ponoreného objemu.

graf
graf graf

4. Klikni na Applet Archimedov zákon, na základe experimentovania zapíš do tabuľky, aká je výsledná vztlaková sila pri ponorení telesa objemu 7 dm3, hustote telesa 916,8 (ľad), hustote kvapaliny 910 kg/m3 (olivový olej), pre rôzne tiažové zrýchlenia. V applete zadaj hodnotu tiažového zrýchlenia podľa tabuľky, stlač tlačidlo „Ponor“ a výslednú vztlakovú silu zapíš do tabuľky zaokrúhlenú na dve desatinné miesta.

Tiažové zrýchlenie (kg/m3)

3,7
(Mars)

8,6
(Venuša)

9,1
(Saturn)

9,81
(Zem)

11
(Neptún)

Vztlaková sila (N)







5. Zvážte, či vztlaková sila v závislosti tiažového zrýchlenia a či rastie alebo klesá. Vyberte správne grafické vyjadrenie závislosti vztlakovej sily od tiažového zrýchlenia.
  
graf
graf graf

6. Klikni na Applet Archimedov zákon, na základe experimentovania zapíš do tabuľky veľkosť ponorenej časti telesa pre hodnoty objemu telesa 6 dm3, hustoty telesa 700 kg/m3 (drevo 1) a hustoty kvapaliny 1025 kg/m3 (morská voda). Ak meníme tiažové zrýchlenie.

Tiažové zrýchlenie (m/s2)

3,7
(Mars)

8,6
(Venuša)

9,81
(Zem)

11
(Neptún)

22,9
(Jupiter)

Ponorený objem telesa (dm3)





7. Prečo nemá zmena tiažového zrýchlenia vplyv na veľkosť ponoreného objemu telesa?

 

Podľa Archimedovho zákona sa tiaž plávajúceho telesa rovná tiaži kvapaliny, ktorá má rovnaký objem ako jeho ponorená časť. Zmenou

tiažového zrýchlenia, nezmeníme tiaž telesa ani tiaž príslušného objemu kvapaliny.

Podľa Archimedovho zákona sa tiaž plávajúceho telesa rovná tiaži kvapaliny, ktorá má rovnaký objem ako jeho ponorená časť. Zmena

tiažového zrýchlenia, nemá vplyv na zmenu tiaže telesa, takže ani na tiaž príslušného objemu kvapaliny.

Podľa Archimedovho zákona sa tiaž plávajúceho telesa rovná tiaži kvapaliny, ktorá má rovnaký objem ako jeho ponorená časť.  Ak sa

zmení tiažové zrýchlenie, zmení sa v rovnakom pomere tiaž telesa i tiaž príslušného objemu kvapaliny.



8. Na teleso s objemom 7 dm3, ktoré je celé ponorené v nafte s hustotou 940 kg/m3, pôsobí vztlaková sila veľkosti 58,562 N. Výpočtom zisti na akej planéte teleso ponárame a výpočet overte appletom.
Venuša (g=8,6 m/s2)
Urán (g=8,9 m/s2)
Saturn (g=9,1 m/s2)

9. Pre ľubovoľne zvolené hodnoty objemu telesa, hustoty kvapaliny a tiažového zrýchlenia v applete vypočítaj hodnotu hustoty telesa X a telesa Y.
Teleso Y je z plexiskla (1180 kg/m3).
Teleso Y je z vosku (980 kg/m3).
Teleso Y je z asfaltu (1300 kg/m3).
Teleso X je z plexiskla (1180 kg/m3).
Teleso X je z vosku (980 kg/m3).
Teleso X je z asfaltu (1300 kg/m3).



10. Pre ľubovoľne zvolené hodnoty objemu telesa, hustoty telesa a tiažového zrýchlenia v applete vypočítaj hodnotu hustoty kvapaliny X a kvapaliny Y.
Kvapalina Y je med (1417,1 kg/m3).
Kvapalina X je ethanol (789,3 kg/m3).
Kvapalina X je chloroform (1483 kg/m3).

Kvapalina X je med (1417,1 kg/m3).

Kvapalina Y je ethanol (789,3 kg/m3).
Kvapalina Y je chloroform (1483 kg/m3).

11. Pre ľubovoľne zvolené hodnoty objemu telesa, hustoty telesa a hustoty kvapaliny v applete vypočítaj veľkosť tiažového zrýchlenia X a Y.
Tiažové zrýchlenie Y je 273,95 m/s2 (Slnko).
Tiažové zrýchlenie X je 3,8 m/s2 (Merkúr).
Tiažové zrýchlenie Y je 1,622 m/s2 (Mesiac).
Tiažové zrýchlenie X je 273,95 m/s2 (Slnko).
Tiažové zrýchlenie Y je 3,8 m/s2 (Merkúr).

Tiažové zrýchlenie X je 1,622 m/s2 (Mesiac).




12. Vztlakovú silu tradične označujeme s indexom a vydrujeme ju vo fyzikálnej jednotke , slovom .




13. Vyber správne znenie Archimedovho zákona.
  
Teleso ponorené do kvapaliny je nadľahčované silou, ktorej veľkosť sa rovná veľkosti vztlakovej sily kvapaliny rovnakého objemu, ako je objem ponorenej časti telesa.
Teleso ponorené do kvapaliny je nadľahčované silou, ktorej veľkosť a smer sa rovná veľkosti a smeru tiažovej sily kvapaliny rovnakého objemu, ako je objem ponorenej časti telesa.
Teleso ponorené do kvapaliny je nadľahčované silou, ktorej veľkosť sa rovná veľkosti tiažovej sily kvapaliny rovnakého objemu, ako je objem ponorenej časti telesa.

14. V závislosti od veľkosti síl Fg a Fv môžu nastať tri prípady (teleso klesá, vznáša sa alebo stúpa), kde Fg - sila tiažová a Fv  - sila vztlaková. Doplň správny výrok:

a)       Ak Fg > Fv → ρt ρk, teleso v kvapaline .

b)     Ak Fg = Fv → ρt ρk, teleso v kvapaline sa .

c)      Ak Fg < Fv → ρt ρk, teleso v kvapaline .

 

15. Na obrázku sú číselne označené sily, ktoré pôsobia na teleso ponorené v nádobe s kvapalinou. Vyber správne označenie týchto síl.

dfg

  

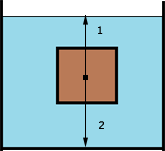
1 - Fg  ;  2 - Fp

1 - Fv   ;  2 - Fp 1 - Fv  ;  2 - Fg 1 - Fg   ;  2 - Fv



16. Vztlaková sila vzniká aj v beztiažovom stave. Je tento výrok pravdivý?

Áno Nie

 

17. Na obrázku sú telesá v ustálenom stave v kvapaline. Doplň správne nasledujúce výroky.

fgh

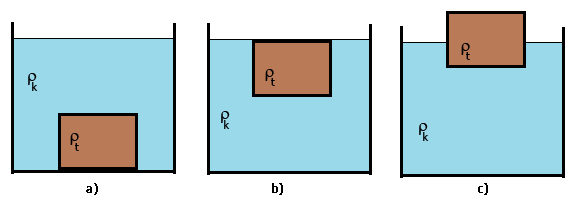
a)  ρk ρt → Fv Fg → teleso

b)  ρk ρt → Fv Fg → teleso sa

c)  ρk  ρt → Fv  Fg → teleso




18. Ponor lode sa zmení ak vypláva z rieky na more. Je tento výrok pravdivý?
Áno Nie

 

19. Koľko percent ľadovca vyčnieva nad voľnou hladinou mora, ak hustota morskej vody je 1025 kg/m3 a hustota ľadu je 918,6 kg/m3?
Nad voľnou hladinou mora vyčnieva % ľadovca.

 

20. Ako Archimedes zisťoval, či kráľovská koruna gréckeho kráľa Hierona je z čistého zlata?
  
Vzal kus  čistého zlata s rovnakou hmotnosťou ako koruna. Zlato pripevnené na silommer vhodil ho do nádoby s vodou a zmeral výslednú pôsobiacu silu. To isté zopakoval s korunou. Ak zlato i koruna pôsobia rovnakou výslednou silou, potom je koruna vyrobená iba zo zlata.
Vzal kus  čistého zlata s rovnakou hmotnosťou ako koruna. Vhodil ho do nádoby s vodou a zmeral objem vody, ktorú tento kus zlata vytlačil.  To isté zopakoval s korunou. Ak zlato i koruna vytlačia rovnaké množstvo vody, potom majú rovnaký objem, ča koruna je teda vyrobená iba zo zlata.
Vzal kus  čistého zlata s rovnakou hmotnosťou ako koruna. Vhodil ho do nádoby s vodou a vypočítal jeho hustotu. To isté zopakoval s korunou. Ak zlato i koruna majú rovnakú hustotu, potom je teda koruna vyrobená zo zlata.

21. V závislosti od veľkosti síl Fg a Fv  môžu nastať tri prípady (teleso klesá, vznáša sa alebo pláva), kde Fg - sila tiažová a Fv  - sila vztlaková. Doplň správne výroky:

a) Teleso z ľadu bude vo vode .

b) Teleso zo skla bude v  nafte .

c) Teleso zo zlata bude v olivovom oleji .

d) Teleso z dreva bude v glycerole .

Na začiatok stránky